comutativa
distributiva
asociativa
distributiva
distributiva
asociativa
distributiva
distributiva
elemento neutro
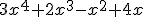
b) identifique 3 elemplos de numeros racionales periodicos y 3 finitos.
racionales periodicos: racionales finitos:
1/2 = 0.5 6/3 = 2
1/4 = 0.25 7/5 = 1.4
3/5 = 0.6 5/2 = 2.5
c)investigar las propiedades de los exponentes:
Propiedades de los exponentes.
El exponente o potencia surge al considerar un número como factor tantas veces como se desee.
an = (a)((a)(a) . . .(a) n veces
n exponente
base x La expresión exponencial xn se llama potencia de n, y se lee como “x a la enésima potencia”, o “x a la potencia n”
Los exponentes indican que un número se esta multiplicando por si mismo n veces.
Así 33 indica que se quiere realizar la operación (3)(3)(3) y se lee 3 al cubo. a2, indica que la base a, se va a multiplicar por sí misma 2 (exponente) veces. Y se lee a al cuadrado. x4 indica que el número x se va a utilizar como factor 4 veces, es decir (x)(x)(x)(x) y se lee x a la cuarta potencia. Para exponentes mayores a 3, se lee, para cualquier variable x, x4;; “x a la cuarta”,x7; “x a la séptima”, y así sucesivamente.
Un número puede descomponerse en n factores deseados
a0 = 1
a1 = a
a2 = aa
a3 = aa2 = aaa
a4 = aa3 = aaaa
an = aan-1 = aa…a n factores
de donde puede obtenerse la regla del producto para los exponentes:
a3 a2 = a3 + 2 = a5
Regla del producto para exponentes:
para toda variable a,b; pertenecientes al conjunto de números naturales, entonces
xaxb = xa + b
Como puedes ver, en un producto de expresiones, se conserva la base y se suman los exponentes.
Se considera importante señalar que la regla del producto para exponentes solo puede utilizarse en aquellas expresiones que tienen la misma variable como base.
¿Por qué, en la expresión x3y4, no se puede aplicar la regla del producto para exponentes?
La regla del producto para exponentes nos indica que su aplicación se debe realizar sobre la misma base o variable. Si la expresión fuera x3x4 ó y3y4 entonces se podría utilizar la regla ya que estaríamos hablando, en estos dos últimos casos, de la misma variable o base elevada a diferente exponente.
Aplicando esta regla puedes ver que
50
Por lo que podemos definir a cualquier variable x0 = 1
Considerando otros ejemplos
(a0)3 = a0 a0 a0 = a0+0+0 = (a0)3 = 1
(a2)5 = a2 a2 a2 a2 a2 = a2 + 2 + 2 + 2 + 2 = (a2)5 = a10
(3 a)2 = (3 a)(3 a) = (3)(3)(a)(a) = 32 a2 = 9 a2
(ab)4 = (ab)(ab)(ab)(ab) = aaaabbbb = a4b4
De los ejemplos anteriores se puede obtener la regla de potencia para los exponentes.
Regla de potencia para los exponentes:
para toda variable a,b;
(xa)b = xab (xy)a = xaya
paray diferente de 0
Hay que tener cuidado en los casos en que la variable x = 0 ya que 00 es un número indefinido. Es decir, la base nunca puede ser cero, en ningún caso.
Es conveniente aprender aquí a expresar el número 1 en términos de fracciones. Dicha forma de expresión será muy útil posteriormente.
Así el 1 puede expresarse como una expresión fraccional donde el denominador es idéntico al numerador.
Todas las expresiones anteriores son equivalentes e iguales a 1. Se vera la utilidad de esto cuando se este trabajando con fracciones, ya que en general cuando se tiene la forma equivalente a la unidad esta puede eliminarse de la expresión algebraica sin alterar el resultado.
Podemos continuar extendiendo las reglas anteriores como sigue:
(32) (3-2)= 32 - 2 = 30 = 1
xmx-m = xm-m = x0 = 1
Para que este resultado sea congruente con las reglas hasta aquí mencionadas, entonces es necesario que x-m, sea el inverso multiplicativo de xm. Es decir que es necesario que , resultado que es congruente con las propiedades mencionadas. Entonces se puede dar la siguiente definición:
Exponente negativo:
Si n es un número entero y x diferente de 0 tenemos que
,
Además se tiene la siguiente regla del cociente:
Regla del cociente
para toda variable x, diferente de cero
Ahora sí tenemos los elementos necesarios para obtener el resultado de
(32) (3-2) = 32 - 2 = 30 = 1, ya que
Para finalizar con este apartado, tenemos el siguiente teorema:
Teorema
para toda variable x,y; diferentes de 0
